This post is also available in Dutch.
The second Donders Education Hackathon will be held this autumn. There, scientists, programmers and teachers will spend 24 hours developing educational games. Florian Krause, a member of last year’s winning team, writes about his experience and the app his team developed.
“As both a researcher in cognitive neuroscience and a developer of open source software used for scientific purposes (Expyriment), I jumped at the opportunity to participate in the Donders Education Hackathon. It was my first hackathon and, after my experience, I can only urge people to join this year’s edition.
During my PhD, I investigated the role of the body in understanding numerical concepts, and developed some interest in the educational implications of this new field. I teamed up with a good friend and colleague at the Donders, Daniel Sheppard, who used to be a teacher in the UK, and two very motivated and talented cognitive science students from the University of Osnabrueck, Renato Garita and Hamza Kebiri.
(Slowly) turning ideas into action
The first few hours of the Hackathon were quite exhausting as we discussed several potential ideas of what to do. It wasn’t until after dinner that we actually started to write some code. However, after an intensive night of work, and just minutes before the deadline the next morning, we had a working prototype of the game we named “MagniShoot.”
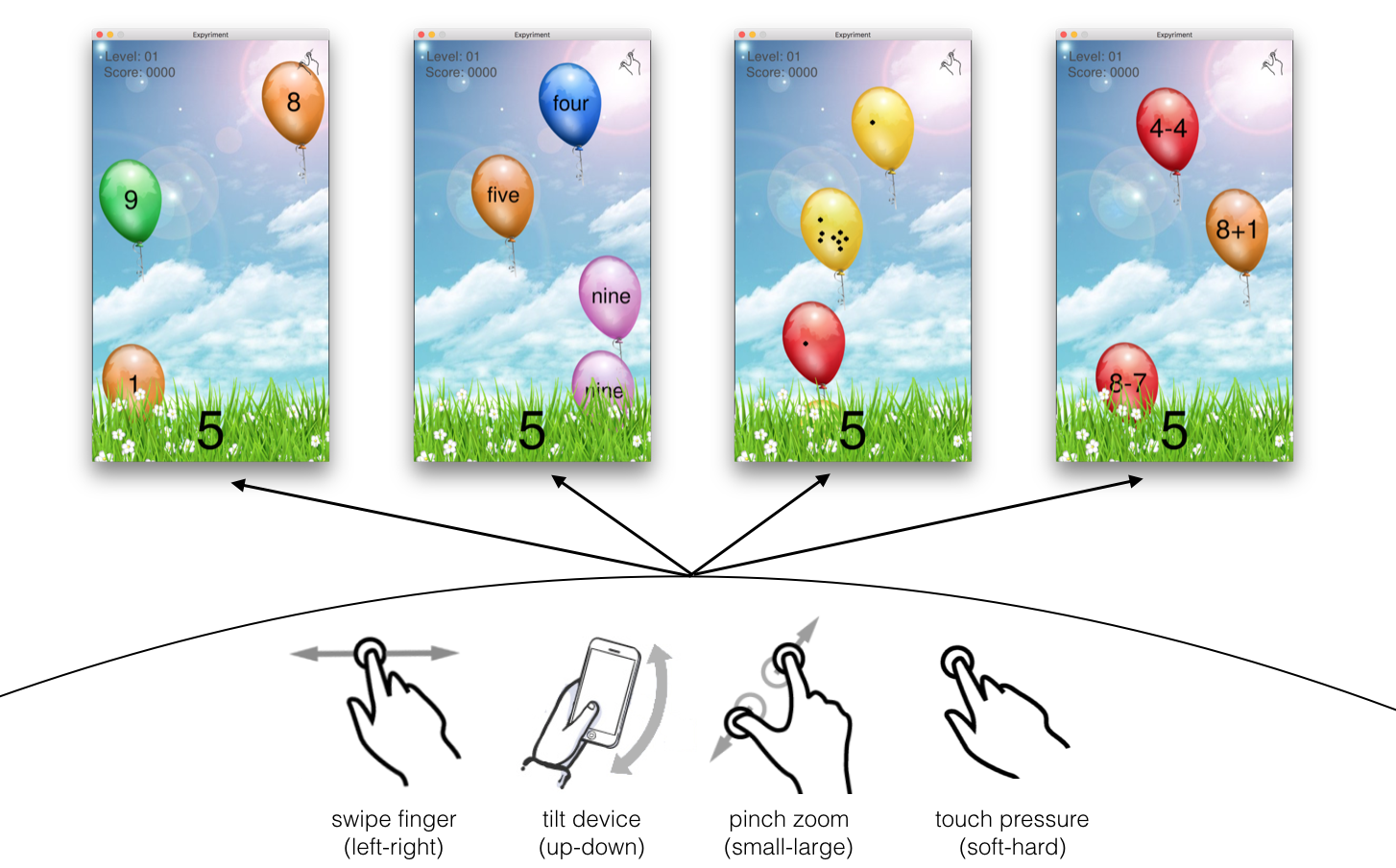
In the game “MagniShoot”, children learn numerical concepts by linking them to something they can experience with their bodies: The player pops floating balloons by producing a numerical value by for example swiping, pinching or pressing the screen.
Learning numerical concepts with the body
Learning something abstract, such as numerical size, calls for a concrete approach in the classroom. For several decades, scientists have assumed that we understand numbers by spatially organising them along a so-called ‘mental number line.’ In primary school education an actual number line is often used as a method to visualise and teach basic numeric principles.
However, more and more research suggests that we also relate numbers to all kinds of other size-related information that we can experience with our body, such as force or physical size, and the degree to which we rely on any one of these bodily representations seems to differ between individuals.
Based on this research, we developed a prototype of an app in which children learn about numerical concepts by actively linking them to not just a number line, but multiple bodily experiences. In this balloon-popping game, children are challenged to manually produce and manipulate numerical values in various playful manners, such as swiping, pinching, and pressing the screen, as well as tilting the device.
We are currently exploring the possibilities to further develop the game with more advanced aspects, such as automatic profiling of children’s performance for parents and teachers to monitor, and adapting the game to individual performance and learning goals.
See this video for a brief demonstration of the game at the end of the Donders Education Hackathon
Surprising results
I was absolutely astonished by the high quality of the solutions that all the teams came up with during the hackathon. In the end, after 24 hours of very hard work, we felt rewarded and satisfied. And not because my team won a prize, but because of what we were all able to achieve together in groups in such a short amount of time.”
The Donders Hackathon is open for people with all kinds of backgrounds. More information about this year’s edition can be found on: www.ru.nl/dondershackathon.
Written by Florian Krause.
Further reading:
Krause, F., Lindemann, O., Toni, I., & Bekkering, H. (2014). Different brains process numbers differently: structural bases of individual differences in spatial and nonspatial number representations. Journal of Cognitive Neuroscience, 26(4), 768–776.
Walsh, V. (2014). A Theory of Magnitude Oxford Handbooks Online A Theory of Magnitude : The Parts that Sum to Number, (December), 1–12. http://doi.org/10.1093/oxfordhb/9780199642342.013.64
