This post is also available in Dutch.
Scientists use statistics in order to generalize findings from small groups of participants to entire populations. Learn how they can do that with the help of a galactic friend.
Have you ever been curious to know the average height of the Dutch population? Using statistics, scientists could confidently give you an answer by looking at the height of just a small group of randomly selected Dutchies, a group much smaller than the entire population. Statistics can provide a lot of answers about our world, even if you’re setting foot on Earth for the first time…
A scientist from outer space
Imagine the following: an alien scientist arrives at our lovely blue planet, wishing to examine its most intelligent species more closely. After some internal debate about dolphins, chimps and elephants, he ends up choosing us, Homo Sapiens.
Let’s name him “Dudu”, after the only audible sound he seems to make.

Dudu is interested in the ratio of males in the human population. The men of his species heavily outnumber the ladies and he suspects that’s the root cause of the many conflicts on his planet. That made him curious about alien civilizations.
The need for statistical inference
Dudu dives into the alien scientific literature and selects a good strategy. He’ll fly around in his UFO, selecting humans at random, and write down their gender.
Dudu then ends up with a list containing the gender of 10 people, 4 of them men. That’s a male ratio of 4/10 = 0.4, suggesting that 60% of the human population is female.
This is what we call descriptive statistics because the ratio describes something about Dudu’s group of 10 people. This process is relatively straightforward. However, it’s not clear whether that descriptive statistic, based on a small group, is also true for everyone else.
That’s why Dudu’s isn’t satisfied. Do humans really have more females than males? He starts feeling jealous. He wants to know how accurate his estimated ratio is. Is it really TRUE for the whole world population?
Luckily, the alien literature also describes a way for him to assess how confident he can be about his estimate. In Earth’s literature, we call it inferential statistics.
Sampling distributions change with the group size
Dudu’s sources suggest he takes a labour-intensive approach if he truly wants to understand inferential statistics. They tell him to measure many more groups of 10 people and then calculate the male ratio for each group. They also tell him to repeat this process, for the same number of groups, but then with 50, 200 and even 500 people in each group.
He performs these measurements with diligence; he cannot wait to uncover the truth! Based on his findings, Dudu then creates four different figures, each from many male ratios estimated from groups of these four different sizes.
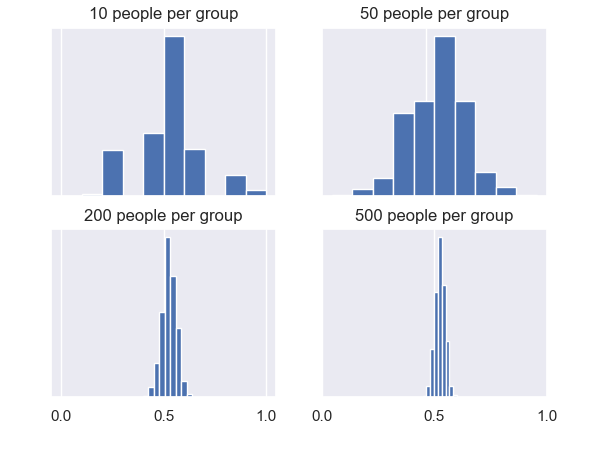
On Earth, these kinds of figures are called histograms. The histograms above show how many of the groups had a certain male ratio (shown on the horizontal axis). The bigger the bar, the more groups had a male ratio corresponding to that bar.
These four collections of male ratios plotted in the figures are each estimated from many groups (also called samples) of people. They are thus appropriately called sampling distributions.
Looking at these figures, Dudu notices two things when the groups have more people in them:
- The curves become increasingly bell-shaped, or normally distributed. This astonishes him because the measurements within the groups themselves look very different.
- These bell-shaped curves become narrower.
Becoming confident about generalizing to the population
After all this work, Dudu finally feels satisfied. He looks at the peak of the bell-shaped curve in the ‘500 people per group’ histogram. This is the average or mean of the sampling distribution. He thinks this mean is currently his best estimate for the true male ratio in the human population.
This is his reasoning: Dudu’s reading taught him that the narrowness of this bell-shaped curve says something about how confident he can be about it. If the curve is very tall and narrow, most of the group ratios are very close to their mean, meaning there is little variation (we also call this variance, spread or deviation) between the ratios, and high confidence that the estimated ratios are close to the ratio of the entire human population.
If Dudu would instead choose the ‘10 people per group’ histogram, he would be choosing a sampling distribution with a wider curve, with lots of variation between group ratios and less confidence. This explains why his original finding of 40% of men was so far off from the real value!
Using a group size of 500 people, Dudu has become confident that the ratio of men is greater than 0.5. For whatever reason, about 0.525 of humans are male. “More men than women!” He concludes. That makes Dudu a little less jealous. He decides to move on to his next star system of interest. Humans have too many idiotic conflicts going on for his taste anyway.
Luckily, we only need one group
Dudu discovered that the variation around the mean of the male ratios of his groups was important. The variation in a sampling distribution is so important, in fact, that humans gave it a unique name: the standard error. And, luckily for science, it’s not necessary to repeat measurements for many groups every time. The standard error can be approximated using the variation between values in only one group!
Dudu also found that using groups containing more people made his sampling distributions narrower, effectively decreasing the standard error. Since a reduction in standard error increases how confident a scientist is that their estimate is close to the true population value, adding more people to an experiment generally improves confidence.
Therefore, when researching the most intelligent species on the next planet he visits, Dudu will choose a bigger group size than just 10 people, one where he feels like his standard error will be low enough. He can then be confident about his estimated male ratio and save himself a lot of work.
And that’s the magic. That’s how scientists on Earth also generalize their experiments from small experimental groups to entire populations.
Credits
Author: Jeroen
Buddy: João
Editor: Mónica
Translator: Felix
Editor translation: Wessel
