This post is also available in Engels.
Kansen en ‘odds’ worden vaak door elkaar gehaald. We hebben er in het Nederlands niet eens verschillende woorden voor; we gebruiken gewoon de Engelse term. Het verschil tussen de twee is echter erg belangrijk. Bijvoorbeeld bij gokspellen, maar ook wanneer je probeert te begrijpen wat de kans is dat je een ziekte kunt krijgen.
Het verschil tussen ‘kansen’ en ‘odds’ is subtiel, maar belangrijk. Dit geldt des te meer in de medische wetenschap: als je hier het risico, dat bepaald wordt aan de hand van kansen, en ‘odds ratios’ door elkaar haalt, kun je misleidende resultaten krijgen.
Zowel kansen als odds reflecteren de kans dat iets wel of niet in de toekomst zal gebeuren. Het zijn allebei ratio’s, die berekend worden via het aantal keer dat een gebeurtenis in het verleden is voorgekomen. Het verschil schuilt echter in de deler; kansen worden bepaald aan de hand van het totale aantal waarnemingen (ongeacht of de gebeurtenis wel of niet is voorgekomen), terwijl odds worden berekend relatief aan het aantal keren dat iets niet gebeurt.
Kansen zijn relatief aan alle waarnemingen
De kans dat een gebeurtenis plaatsvindt, wordt berekend als de ratio van het aantal keren dat de gebeurtenis plaatsvond en het aantal keer dat er is gemeten (alle waarnemingen).
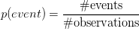
Kansen liggen altijd tussen de 0 en de 1. Iets kan niet gebeuren met een kans van meer dan 100%, want met 100% kans, gebeurt het al altijd. Het kan ook niet plaatsvinden met een kans kleiner dan 0%, want met 0% kans, gebeurt het nooit.
Als je een normale dobbelsteen zou gooien, zou hij altijd op een kant landen met een kans van 1/6.
Odds zijn relatief aan niet-gebeurtenissen
De odds dat een gebeurtenis plaatsvindt, worden berekend als de ratio van het aantal keren dat de gebeurtenis plaatsvond en het aantal keren dat de gebeurtenis niet plaatsvond.
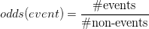
Odds groter dan 1 betekenen dat er meer waarnemingen waren waar iets wel gebeurde, dan dat er waarnemingen waren waar iets niet gebeurde.
Odds zijn nuttig als je aan het gokken bent en wilt weten of “je het geluk mee of tegen hebt”. Als je gokt dat je een 6 zal dobbelen, dan is de kans dat je wint 1/6, terwijl je odds op winnen 1/5 zijn.
Dus de odds zijn 5 tegen 1, wat betekent dat het vijf keer zo waarschijnlijk is dat je zal verliezen dan dat je zal winnen.
Relatief risico op blootstelling tijdens een epidemie
In het voorbeeld van de dobbelstenen weten we de kansen en de odds omdat we weten hoe de dobbelsteen werkt (als er natuurlijk niet mee gesjoemeld is). In de medische wetenschap weten we dit soort dingen vaak niet. Er zijn dan ook veel studies die achter deze kansen en odds proberen te komen, vooral in epidemiologie.
Stel je voor dat er een epidemie is waar veel mensen een virus hebben opgelopen. Veel van hen sterven gedurende een jaar. Ondertussen sterven er andere mensen, die het virus niet hebben opgelopen, aan andere dingen.
Een interessante vraag zou dan zijn: hoeveel neemt iemands risico op overlijden toe, als ze blootgesteld zijn aan het virus? Dit wordt benaderd door het relatieve risico (RR), wat hier neerkomt op de ratio van de kans dat je doodgaat als je het virus hebt opgelopen tegen de kans dat je doodgaat als je het virus niet hebt opgelopen.
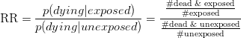
Het RR zegt iets over het gevaar van blootstelling aan het virus (dus hoe sterk het effect van het virus is) en is redelijk eenvoudig te begrijpen. Als de kans op overlijden in een jaar, na blootstelling aan het virus, 60% is, terwijl het normaal 20% is, dan zal het RR 3 zijn (0.6/0.2). In dat geval, is doodgaan na blootstelling aan het virus 3 keer zo waarschijnlijk dan doodgaan door andere oorzaken.
Hoe zit het met de odds ratio?
Je kan ook berekenen hoeveel je odds op overlijden toenemen door de odds ratio (OR) te berekenen. De OR is soms beter te toepasbaar en zegt ook iets over de sterkte van een effect.
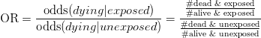
De odds op overlijden na blootstelling zijn 3/2 (60% kans dat je overlijdt en 40% kans dat je blijft leven) en als je niet blootgesteld bent, zijn ze 1/4 (20% kans op overlijden, en 80% kans dat je blijft leven). Dat geeft een OR van 1.5/0.25 = 6.
Deze OR is wat moeilijker te begrijpen. Dat is waarom mensen de OR soms zien als het RR, die wat intuïtiever is. Maar de OR en het RR kunnen erg anders zijn, vooral als blootstelling een groot effect heeft op bevolkingsgroepen die al een hoog risico lopen op overlijden. Dat komt doordat voor deze groepen de odds veel groter worden dan de kansen. Dat gebeurde ook in ons voorbeeld, waar de odds op overlijden na blootstelling (3/2) veel groter waren dan de kans (0.6). Zo werd de OR twee keer zo groot als het RR!
Kies voorzichtig!
Dus waarom zou je niet gewoon altijd het RR gebruiken? De OR heeft wat voordelen over het RR, zoals bepaalde statistische eigenschappen. Maar vooral: de OR kan soms gebruikt worden waar het RR niet werkt.
Dat is bijvoorbeeld in case-control onderzoeken, waar mensen met een bepaalde conditie vergeleken worden met gezonde mensen. Hier selecteren wetenschappers een aantal mensen die een ziekte hebben opgelopen (de cases), waarna ze kijken hoe vaak deze mensen blootgesteld zijn aan een virus. Vervolgens nemen de wetenschappers een groep mensen die de ziekte niet hebben opgelopen en kijken ze hoe vaak deze groep is blootgesteld aan het virus. Nu kunnen de wetenschappers de OR berekenen, omdat ze weten hoe vaak mensen wel en niet zijn blootgesteld in elke groep. Ze kunnen echter niet berekenen wat het RR is, omdat ze niet weten wat het totaal aantal mensen in de bevolking is dat wel of niet is blootgesteld aan het virus.
De OR en het RR zijn beiden waardevol, maar het is belangrijk om te onthouden dat het andere maatstaven zijn. En hoewel ze vaak vergelijkbaar zijn, kunnen ze soms flink verschillen. Als je een goede keuze wilt maken in een behandeling of een strategie voor de volksgezondheid, is het uitermate belangrijk dat je deze kansen goed gebruikt. We moeten een nauwkeurig beeld van de wereld hebben als we de kansen in ons voordeel willen gebruiken.
Credits
Originele taal: Engels
Auteur: Jeroen
Buddy: Mónica
Editor: Christienne
Vertaler: Wessel
Editor Vertaling: Jill
Afbeelding verkregen van Alex Chambers via Unsplash.
