This post is also available in Engels.
Als ik je zou vertellen dat kunstwerken zoals schilderijen en muziek prachtig zijn, zal dat niets nieuws zijn. Je kunt waarschijnlijk zelfs zien hoe de term schoonheid nog breder toegepast kan worden, bijvoorbeeld op de natuur of natuurlijke fenomenen, op poëzie en emoties. Maar nu wil ik je graag aan een andere vorm van uiterste schoonheid voorstellen: wiskunde. Bereid je voor om je door de pure pracht en praal van wiskundige formules te laten overspoelen.
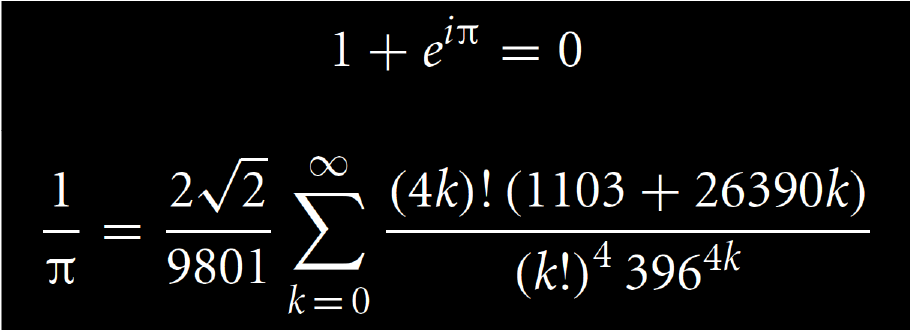
Net als het waarderen van kunst
Hoewel een wiskundige formule waarschijnlijk niet het eerste is waar je aan denkt als ik je vraag om aan iets prachtigs te denken, hebben al veel mensen (waaronder veel wiskundigen en natuurkundigen) hun ervaring van wiskundige schoonheid beschreven. Deze beschrijvingen geven aan dat de waarneming van zulke schoonheid mogelijk niet anders is dan bijvoorbeeld visuele of muzikale schoonheid. Sommige hebben zelfs geprobeerd uit te leggen waarom het mogelijk is dat je een wiskundige formule wel of niet leuk vindt, door wenselijke kwaliteiten te definiëren. Voorbeelden van kwaliteiten die bijdragen aan wiskundige schoonheid zijn elegantie, eenvoud, duidelijkheid, beknoptheid, originaliteit, belang en universeel nut. Je kunt, interessant genoeg, ten minste een deel van deze kwaliteiten gebruiken om te beschrijven waarom je een schilderij of een liedje mooi vindt.
Daarnaast heeft recent onderzoek aangetoond dat wiskundigen hersenactiviteit vertoonden in de mediale orbitofrontale cortex als ze wiskundige formules zagen. Maar dat gebeurde alleen als ze de formule eerder hadden bestempeld als ‘prachtig’ en niet als ze de formule lelijk vonden. Dat deel van het brein is ook geactiveerd als mensen schilderijen of muziek bewonderen. Sterker nog, de hoeveelheid activiteit in de hersenen kwam overeen met de mate waarin een kunststuk of formule esthetisch bevonden werd. Deze onderzoeken laten zien dat we in staat zijn verschillende soorten waargenomen schoonheid te meten.
Voor iedereen
Je denkt nu vast dat het waarderen van wiskundige formules alleen iets is voor wiskundigen en andere cijfer-aficionado’s. In andere woorden: schoonheid schuilt in het oog van de waarnemer, die in dit geval een wiskundige is. Dat is ook wat onderzoekers en filosofen al jaren zeggen: hoewel visuele en muzikale schoonheid waarnemings-gebaseerd zijn, is wiskundige schoonheid meer abstract en gebaseerd op kennis. Dit zou betekenen dat het waarnemen van wiskundige schoonheid sterk afhangt van de waarnemer en veel kan verschillen tussen personen. Hier staat tegenover dat in de bovengenoemde studie de waarderingen van de wiskundige formules niet echt subjectlief lijken te zijn, maar juist consistent zijn voor alle deelnemers. Dit kan natuurlijk komen doordat alle deelnemers soortgelijke kennis van wiskunde en begrip van de formules hebben. Deze uitleg wordt echter niet ondersteund door een andere studie onder leken. Deze nieuwe studie liet gemiddelde Amerikanen de schoonheid bepalen van wiskundige argumenten (bewijzen van een wiskundige stelling), schilderijen en klassieke muziekstukken. Deze beoordeling was volledig subjectief en gebaseerd op intuïtie. Verbazingwekkend genoeg waren deelnemers het niet alleen eens over de pracht van de schilderijen en muziekstukken, maar ook over de schoonheid van de wiskundige argumenten. Misschien zijn er dus wel manieren om bepaalde delen van wiskunde aantrekkelijker te maken voor jonge leerlingen en ze te motiveren om de wiskunde in te gaan.
Originele taal: Engels
Auteur: Eva Klimars
Buddy: Francie Manhardt
Editor: Marisha Manahova
Vertaler: Wessel Hieselaar
Editor Vertaling: Jill Naaijen
De uitgelichte afbeelding is gecreëerd door Robert Webbs Stella software (http://www.software3d.com/Stella.php).