This post is also available in Engels .
Wetenschappers gebruiken statistiek om hun bevindingen te kunnen generaliseren van kleine groepjes proefpersonen naar volledige bevolkingsgroepen. Leer hier van een galactische vriend hoe ze dat doen.
Ben je ooit wel eens nieuwsgierig geweest naar de gemiddelde lengte van Nederlanders? Met behulp van statistiek kunnen wetenschappers je daar een overtuigend antwoord op geven door te kijken naar de lengte van slechts een kleine groep willekeurig geselecteerde Hollanders, een veel kleinere groep dan de daadwerkelijke bevolking. Statistiek kan je een hoop zeggen over onze wereld, zelfs als je voor het eerst een voet zet op Aarde…
Een wetenschapper uit de ruimte
Stel je het volgende voor: een buitenaardse wetenschapper komt naar onze prachtige blauwe planeet om haar meest intelligente bewoners eens goed te bestuderen. Na wat getwijfel over dolfijnen, chimpansees en olifanten kiest hij uiteindelijk voor ons: Homo Sapiens.
Laten we deze wetenschapper “Dudu” noemen: het enige geluid dat hij lijkt te kunnen maken.

Dudu is geïnteresseerd in de man-vrouwverhouding van de menselijke bevolking. In zijn eigen soort zijn er veel meer mannen dan vrouwen en hij vermoedt dat dit de oorsprong is van de vele conflicten op zijn planeet. Daarom is hij nieuwsgierig naar andere beschavingen.
Waarom statistische inferentie nodig is
Dudu duikt in de ‘buitenaardse’ wetenschappelijke literatuur en kies een goede strategie. Hij besluit een beetje rond te gaan vliegen in zijn UFO, willekeurig mensen te selecteren en hun geslacht op te schrijven.
Zo komt Dudu aan een lijst met het geslacht van 10 mensen, onder wie 4 mannen. Dat is een proportie van mannen van 4/10 = 0.4, wat suggereert dat 60% van de populatie vrouwelijk is.
Dit noemen we beschrijvende statistiek omdat de verhouding iets beschrijft over Dudu’s groep van 10 personen. Dit proces is relatief eenvoudig. Het is echter onduidelijk of beschrijvende statistiek, die gebaseerd is op een kleine groep, ook waar is voor alle anderen in de bevolkingsgroep.
Dudu is daarom nog niet tevreden. Zijn er echt meer vrouwelijke dan mannelijke mensen? Hji begint jaloers te worden. Hij wil weten hoe accuraat zijn geschatte proportie is. Geldt deze echt voor de GEHELE wereldbevolking?
Gelukkig beschrijft de literatuur ook een manier om na te gaan hoe zeker hij kan zijn van zijn schatting. Op Aarde noemen we dat inferentiële (of gevolgtrekkende) statistiek.
De groepsgrootte verandert de verdeling van de steekproef
Dudu’s bronnen suggereren dat hij een arbeidsintensieve aanpak dient te gebruiken als hij inferentiële statistiek echt wilt begrijpen. Ze vertellen hem dat hij nog veel meer groepen van 10 mensen moet meten en de man-vrouwverhouding voor elke groep moet berekenen. Ook moet hij dit proces meerdere keren doorlopen, met dezelfde hoeveelheid groepen, maar dan met groepen van 50, 200 en zelfs 500 mensen per groep.
Hij voert dit nauwkeurig uit; hij kan niet wachten om de waarheid te onthullen! Op basis van zijn bevindingen maakt hij de onderstaande vier afbeeldingen, elk het gevolg van veel man-vrouwverhoudingen die zijn geschat vanuit groepen van deze vier verschillende groepsgroottes.
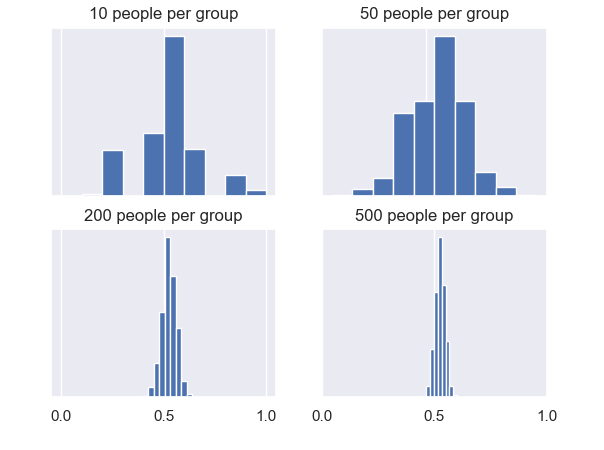
Op Aarde noemen we dit soort figuren een histogram. De histogrammen hierboven laten zien hoeveel van de groepen (verticale as) een bepaalde man-vrouwverhouding hadden (horizontale as). Hoe groter de staaf, hoe meer groepen een verhouding hadden van die specifieke staaf.
Deze vier verzamelingen van man-vrouwverhoudingen zijn elk geschat van veel groepen (ook wel steekproeven) van mensen. Ze worden dus ook wel steekproefverdelingen genoemd.
Het valt Dudu op dat er twee dingen veranderen naarmate de groepsgrootte toeneemt:
- De verdelingen zijn meer klokvormig, of normaal verdeeld. Dit verbaast hem want de metingen binnen de individuele groepen zien er heel anders uit.
- Deze klokvormige verdelingen worden steeds smaller.
Zeker worden over generalisatie naar de populatie
Na al dit werk is Dudu eindelijk tevreden. Hij kijkt naar de piek van de klokvormige verdeling in het ‘500 mensen per groep’ histogram. Dit is het gemiddelde van de steekproefverdeling. Hij denkt dat het gemiddelde op het moment de beste inschatting is van de daadwerkelijke man-vrouwverdeling in de gehele wereldbevolking.
Dit is zijn logica: Dudu’s literatuuronderzoek leerde hem dat de breedte van de verdeling iets zegt over hoe zeker (of nauwkeurig) de schatting is. Als de verdeling erg lang en smal is zijn de meeste verhoudingen erg dichtbij het gemiddelde, wat betekent dat er weinig variatie is (we noemen dit ook wel variantie, spreiding, of afwijking) tussen de verhoudingen, en er een hoge zekerheid is dat de geschatte verhoudingen dichtbij de verhoudingen van de gehele bevolking liggen.
Als Dudu in plaats daarvan het ’10 mensen per groep’ histogram zou kiezen, zou hij gaan voor een veel brede steekproefverdeling met veel meer variatie tussen groepen en minder zekerheid. Dit verklaart waarom zijn originele resultaat met 40% mannen zo sterk afweek van de daadwerkelijke waarde!
Door een groepsgrootte van 500 mensen te gebruiken kan Dudu er zeker van zijn dat de man-vrouwverhouding hoger is dan 0.5. Om wat voor reden dan ook zijn ongeveer 52.5% van alle mensen man. “Meer mannen dan vrouwen!” concludeert hij. Dat maakt hem iets minder jaloers. Hij besluit door te gaan naar het volgende sterrenstelsel. Mensen op Aarde hebben naar zijn smaak toch al te veel onzinnige conflicten met elkaar.
Gelukkig hebben we maar 1 groep nodig
Dudu ontdekte dat de variatie rondom de gemiddelde man-vrouwverhouding belangrijk is. De variatie in een steekproefverdeling is zelfs zo belangrijk, dat mensen het een speciale naam hebben gegeven: de standaardfout. En, gelukkig voor de wetenschap, is het niet nodig om de meting voor heel veel groepen te herhalen. De standaardfout kan worden geschat met behulp van de variatie tussen verschillende waardes in een enkele groep!
Dudu vond ook dat groepen met meer mensen smallere steekproefverdelingen gaven, wat in feite de standaardfout kleiner maakt. Omdat een kleinere standaardfout de zekerheid vergroot waarmee de wetenschapper kan concluderen dat zijn schatting dichtbij de daadwerkelijke waarde zit, zorgt het meten van meer proefpersonen over het algemeen voor meer zekerheid.
Daarom zal Dudu tijdens zijn bezoek aan intelligente soorten van andere planeten grotere groepsgroottes kiezen dan van slechts 10 mensen. Hij zal een groepsgrootte kiezen waarvan hij denkt dat de standaardfout klein genoeg is. Dan kan hij zekerder zijn over zijn geschatte man-vrouwverhouding en zichzelf een hoop werk besparen.
En dat is het trucje. Dat is hoe wetenschappers op Aarde ook hun bevindingen generaliseren van een kleine experimentele groep naar gehele bevolkingsgroepen.
Credits
Author: Jeroen
Buddy: João
Editor: Mónica
Translator: Felix
Editor translation: Wessel

mooi verhaal maar zal het waar zijn ben benieuwd hoe het eindigt…